Criado por Tony Hoare, o Quicksort (ordenação rápida) é um algoritmo de ordenação recursivo de divisão e conquista.
Uma das suas vantagens é que a ordenação é realizada no próprio vetor (in-place). Isso significa que não há necessidade de alocar memória auxiliar para realizar a ordenação.
Sua complexidade no tempo é $O(n\log n)$ no melhor caso e no caso médio e $O(n^2)$ no pior caso. Contudo, em geral, o Quicksort apresenta um desempenho superior a outros algoritmos similares, como o Merge Sort.

Índice
Funcionamento do Quicksort
O Quicksort utiliza a seguinte lógica recursiva para ordenar um vetor [2]
- Se o vetor só possui um elemento (caso base):
- O vetor já está ordenado, retorne-o
- Senão
- Escolha um elemento do vetor, que chamaremos de pivô;
- Divida o vetor em duas partições:
- Uma partição (à esquerda) com os elementos menores ou iguais ao pivô;
- Uma partição (à direita) com os elementos maiores que o pivô;
- Reaplique o método nas duas partições.
Como não existe uma regra para a escolha do pivô, então existem várias verões do Quicksort. A versão original, de Hoare, escolhe o primeiro elemento do vetor como pivô. Em Algoritmos: teoria e prática, Cormen [1] apresenta uma versão que utiliza o último elemento como pivô.
A versão de Hoare, em pseudocódigo, é dada a seguir
01. quicksort(A[0...n - 1], inicio, fim) //Quicksort de Hoare 02. | se(inicio < fim) 03. | | q = particao(A, inicio, fim) //realiza a partição 04. | | quicksort(A, inicio, q - 1) /ordena a partição esquerda 05. | | quicksort(A, q + 1, fim) //ordena a partição direita 06. | fim_se 07. fim_quicksort
O algoritmo de partição (particao) é
01. particao(A[0...n - 1], inicio, fim) //partição de Hoare 02. | pivo ← A[inicio] //o pivô é o primeiro elemento 03. | i ← inicio + 1 //índice i faz a varredura da esquerda para direita 04. | j ← fim índice j faz a varredura da direita para esquerda 05. | enquanto(i ≤ j) //enquanto os índice não se ultrapassarem 06. | | enquanto(i ≤ j E A[i] ≤ pivo) //enquanto A[i] não for maior que o pivô 07. | | | i ← i + 1 08. | | fim_enquanto 09. | | enquanto(i ≤ j E A[j] > pivo) //enquanto A[j] não for menor ou igual ao pivô 10. | | | j ← j - 1 11. | | fim_enquanto 12. | | se(i < j) 13. | | | trocar(A, i, j) //se os índices não se ultrapassarem, troque os elementos 14. | | fim_se 15. | fim_enquanto 16. | trocar(A, inicio, j) //coloca o pivô na posição de ordenação 17. | retorne j; 28. fim_particao
Como exemplo, vamos considerar o seguinte vetor

Na primeira chamada recursiva, teremos o 4 como pivô. O processo de particionamento é ilustrado a seguir
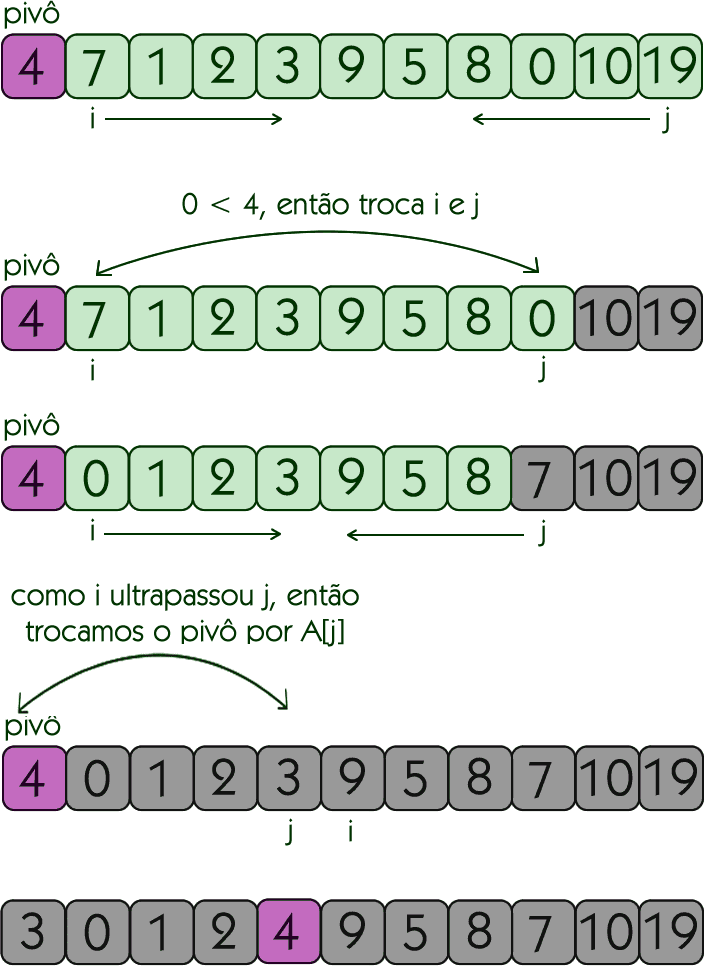
Após a partição, o pivô passa a ocupar a posição correta, isto é, a posição onde ele deve estar ao final da ordenação. Agora, temos duas partições (ou subvetores) para ordenar. Basta reaplicar o Quicksort recursivamente em ambos os vetores.
Complexidade assintótica
O melhor caso do Quicksort ocorre quando as partições são balanceadas, isto é, cada partição com $n/2$ elementos. A equação de recorrência nesse caso é igual a do Merge Sort
$$T(n)=2T(n/2)+\Theta(n)\quad(\text{melhor caso})$$
$\Theta(n)$ é a complexidade no tempo do método de partição. A solução dessa recorrência é $T(n)=\Theta(n\log n)$ ou, equivalentemente, $T(n)=O(\log n)$ e pode ser obtida através do teorema mestre ou pelo método de Akra-Bazzi.
Já o pior caso do Quicksort ocorre quando as chamadas recursivas produzem partições com $0$ e $n-1$ elementos. A partição de tamanho zero fica à direita ou à esquerda do pivô (depende do vetor).
Nas versões de Hoare e Cormen, esse caso patológico ocorre quando o array está ordenado em ordem crescente ou descrente. A equação de recorrência desse caso é
$$T(n)=T(n-1)+\Theta(n)\quad(\text{pior caso})$$
A solução dessa recorrência é $T(n)=O(n^2)$, que é a mesma complexidade (no pior caso) do Bubble Sort, Insertion Sort e Selection Sort. Esse é o ponto fraco do Quicksort. Embora existam várias versões do algoritmo que tentam minimizar esse pior caso, sempre haverá alguma configuração na qual o Quicksort será $O(n^2)$.
A complexidade no caso médio do Quicksort é $O(n\log n)$ e é um dos pontos fortes do algoritmo. O caso médio é uma medida estatística. Isso significa que, ao executar o Quicksort, espera-se que o tempo de execução seja $O(n\log n)$.
É claro, o Merge Sort também é $O(n\log n)$. Entretanto, na prática, o Quicksort normalmente é mais rápido que o Merge Sort, pois a notação assintótica oculta as constantes multiplicativas e os termos de menor ordem de grandeza que são determinantes ao comparar algoritmos com a mesma complexidade. A dedução dessa complexidade está disponível no livro Algoritmos: teoria de prática [1].
O gráfico a seguir faz um comparativo entre o Merge Sort, o Quicksort e o Heapsort ao ordenar vetores aleatorizados. Observe que o Quicksort é mais rápido que os outros dois algoritmos.

Códigos
Você pode baixar o Quicksort de Hoare em Java, C e em JavaScipt nos links abaixo ou pode simplesmente copiar os códigos incorporados no artigo. Adicionalmente, também disponibilizo a versão de Cormen.
Quicksort de Hoare
Em Java:
//GitHub: HenriqueIni //https://www.blogcyberini.com/ //Versão de Hoare do Quicksort public class QuicksortHoare { //Facilita a vida: só pede o array como argumento public static void quicksort(int[] A){ quicksort(A, 0, A.length - 1); } //Quicksort de Hoare private static void quicksort(int[] A, int inicio, int fim){ if(inicio < fim){ //realiza a partição int q = partition(A, inicio, fim); //ordena a partição esquerda quicksort(A, inicio, q - 1); //ordena a partição direita quicksort(A, q + 1, fim); } } //Método de partição private static int partition(int[] A, int inicio, int fim){ //o pivo é o elemento inicial int pivo = A[inicio]; //índice i irá percorrer o array da esquerda para a direita int i = inicio + 1; //índice j irá percorrer o array da direita para a esquerda int j = fim; //O loop irá parar quando os índices se ultrapassarem while(i <= j){ /* * Este laço irá parar quando encontrar algum elemento * à esquerda que é maior que o pivô, pois ele deveria estar na * partição direita */ while(i <= j && A[i] <= pivo){ i = i + 1; } /* * Esse laço irá parar quando encontrar algum elemento * à direira que é menor ou igual ao pivô, pois ele deveria estar na * partição esquerda */ while(i <= j && A[j] > pivo){ j = j - 1; } //se os índices não ultrapassarem, troca-os de posição if(i < j){ swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, inicio, j); return j; //retorna a posição do pivô } //método auxiliar para realizar as trocas de elementos private static void swap(int[] A, int i, int j){ int temp = A[i]; A[i] = A[j]; A[j] = temp; } }
Em C:
//GitHub: HenriqueIni //https://www.blogcyberini.com/ #include <stdio.h> #include <stdlib.h> //***********************FUNÇÕES AUXILIARES*********************** //função auxiliar para realizar as trocas de elementos void swap(int A[], int i, int j){ int temp = A[i]; A[i] = A[j]; A[j] = temp; } //***********************QUICKSORT DE HOARE****************************** //Partição de Hoare int hoarePartition(int A[], int inicio, int fim) { //o pivo é o elemento inicial int pivo = A[inicio]; //índice i irá percorrer o array da esquerda para a direita int i = inicio + 1; //índice j irá percorrer o array da direita para a esquerda int j = fim; //O loop irá parar quando os índices se ultrapassarem while (i <= j) { /* * Este laço irá parar quando encontrar algum elemento * à esquerda que é maior que o pivô, pois ele deveria estar na * partição direita */ while (i <= j && A[i] <= pivo) { i = i + 1; } /* * Esse laço irá parar quando encontrar algum elemento * à direira que é menor ou igual ao pivô, pois ele deveria estar na * partição esquerda */ while (i <= j && A[j] > pivo) { j = j - 1; } //se os índices não ultrapassarem, troca-os de posição if (i < j) { swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, inicio, j); return j; //retorna a posição do pivô } //Quicksort de Hoare void quicksortHoare(int A[], int inicio, int fim) { if (inicio < fim) { //realiza a partição int q = hoarePartition(A, inicio, fim); //ordena a partição esquerda quicksortHoare(A, inicio, q - 1); //ordena a partição direita quicksortHoare(A, q + 1, fim); } }
Em JavaScript:
//GitHub: HenriqueIni //https://www.blogcyberini.com/ //método auxiliar: troca os elementos i e j em A function swap(A, i, j) { var temp = A[i]; A[i] = A[j]; A[j] = temp; } //***********************QUICKSORT DE HOARE****************************** //Quicksort de Hoare function quicksortHoare(A, inicio, fim) { if (inicio < fim) { //realiza a partição var q = hoarePartition(A, inicio, fim); //ordena a partição esquerda quicksortHoare(A, inicio, q - 1); //ordena a partição direita quicksortHoare(A, q + 1, fim); } } function hoarePartition(A, inicio, fim) { //o pivo é o elemento inicial var pivo = A[inicio]; //índice i irá percorrer o array da esquerda para a direita var i = inicio + 1; //índice j irá percorrer o array da direita para a esquerda var j = fim; //O loop irá parar quando os índices se ultrapassarem while (i <= j) { /* * Este laço irá parar quando encontrar algum elemento * à esquerda que é maior que o pivô, pois ele deveria estar na * partição direita */ while (i <= j && A[i] <= pivo) { i = i + 1; } /* * Esse laço irá parar quando encontrar algum elemento * à direira que é menor ou igual ao pivô, pois ele deveria estar na * partição esquerda */ while (i <= j && A[j] > pivo) { j = j - 1; } //se os índices não ultrapassarem, troca-os de posição if (i < j) { swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, inicio, j); return j; //retorna a posição do pivô }
Quicksort de Cormen
Em Java:
//GitHub: HenriqueIni //https://www.blogcyberini.com/ //Versão do Quicksort do Cormen (Algoritmos: teoria e prática) public class QuicksortCormen { //Facilita a vida: só pede o array como argumento public static void quicksort(int[] A){ quicksort(A, 0, A.length - 1); } //Quicksort de Cormen private static void quicksort(int[] A, int inicio, int fim){ if(inicio < fim){ //realiza a partição int q = partition(A, inicio, fim); //ordena a partição esquerda quicksort(A, inicio, q - 1); //ordena a partição direita quicksort(A, q + 1, fim); } } //Método de partição private static int partition(int[] A, int inicio, int fim){ //o pivo é o elemento final int pivo = A[fim]; int i = inicio - 1; /* * Este laço irá varrer os vetores da esquerda para direira * procurando os elementos que são menores ou iguais ao pivô. * Esses elementos são colocados na partição esquerda. */ for(int j = inicio; j <= fim - 1; j++){ if(A[j] <= pivo){ i = i + 1; swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, i + 1, fim); return i + 1; //retorna a posição do pivô } //método auxiliar para realizar as trocas de elementos private static void swap(int[] A, int i, int j){ int temp = A[i]; A[i] = A[j]; A[j] = temp; } }
Em C:
//GitHub: HenriqueIni //https://www.blogcyberini.com/ #include <stdio.h> #include <stdlib.h> //função auxiliar para realizar as trocas de elementos void swap(int A[], int i, int j){ int temp = A[i]; A[i] = A[j]; A[j] = temp; } //***********************QUICKSORT DE CORMEN****************************** //Partição de Cormen int cormenPartition(int A[], int inicio, int fim) { //o pivo é o elemento final int pivo = A[fim]; int i = inicio - 1; int j; /* * Este laço irá varrer os vetores da esquerda para direira * procurando os elementos que são menores ou iguais ao pivô. * Esses elementos são colocados na partição esquerda. */ for (j = inicio; j <= fim - 1; j++) { if (A[j] <= pivo) { i = i + 1; swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, i + 1, fim); return i + 1; //retorna a posição do pivô } //Quicksort de Cormen void quicksortCormen(int A[], int inicio, int fim) { if (inicio < fim) { //realiza a partição int q = cormenPartition(A, inicio, fim); //ordena a partição esquerda quicksortCormen(A, inicio, q - 1); //ordena a partição direita quicksortCormen(A, q + 1, fim); } }
Em JavaScript:
//método auxiliar: troca os elementos i e j em A function swap(A, i, j) { var temp = A[i]; A[i] = A[j]; A[j] = temp; } //***********************QUICKSORT DE CORMEN****************************** //Partição de Cormen function cormenPartition(A, inicio, fim) { //o pivo é o elemento final var pivo = A[fim]; var i = inicio - 1; var j; /* * Este laço irá varrer os vetores da esquerda para direira * procurando os elementos que são menores ou iguais ao pivô. * Esses elementos são colocados na partição esquerda. */ for (j = inicio; j <= fim - 1; j++) { if (A[j] <= pivo) { i = i + 1; swap(A, i, j); } } //coloca o pivô na posição de ordenação swap(A, i + 1, fim); return i + 1; //retorna a posição do pivô } //Quicksort de Cormen function quicksortCormen(A, inicio, fim) { if (inicio < fim) { //realiza a partição var q = cormenPartition(A, inicio, fim); //ordena a partição esquerda quicksortCormen(A, inicio, q - 1); //ordena a partição direita quicksortCormen(A, q + 1, fim); } }
Referências
- [1] CORMEN, T. H. et al. Algoritmos: teoria e prática. 3 ed. Rio de Janeiro: Elsevier, 2012.
- [2] GOODRICH, M. T., TAMASSIA, R.. Data Structures and Algorithms in Java. 5 ed. Porto Alegre: Bookman, 2013.

Ótimo conteudo
ResponderExcluirObrigado!
Excluir