Questões do POSCOMP sobre Linguagens Formais e Autômatos #02

Nesta postagem, apresento algumas questões resolvidas do POSCOMP dos anos 2004, 2005, 2007 e 2008 sobre Linguagens Formais e Autômatos.

Para mais questões resolvidas, acesse a página POSCOMP.

POSCOMP 2004

A questão a seguir é do ano 2004.

Questão 62

Seja a seguinte linguagem, onde $\epsilon$ representa a sentença vazia

$$\begin{align*}S&\rightarrow AB\,|\,CD\\A&\rightarrow a\,|\,\epsilon\\B&\rightarrow b\,|\,f\\C&\rightarrow c\,|\,g\\D&\rightarrow h\,|\,i\end{align*}$$

Qual o conjunto de terminais que podem começar sentenças derivadas de $S$?

• (A) $\{a, c, g\}$
• (B) $\{a, b, f, c, g\}$
• (C) $\{a, b, f, c, g, h, i\}$
• (D) $\{a, c, g, h, i\}$
• (E) $\{a, b, f\}$

Resolução

Na prática, o enunciado solicita o conjunto FIRST de S.

Todos os terminais que iniciam sentenças produzidas pelos não terminais A e C fazem parte do conjunto: $\{a, c, g\}$. Como A produz a cadeia vazia, então devemos também incluir os não terminais que iniciam sentenças produzidas pelo não terminal B: $\{b, f\}$.

Unindo os conjuntos, temos: $\{a, b, c, f, g\}$. Portanto, a alternativa correta é a B.

POSCOMP 2005

A questão a seguir é do ano 2005.

Questão 28

Qual das seguintes afirmações é falsa?

• (A) Dada uma máquina de Turing M com alfabeto de entrada $\Sigma$ e uma string $w\in\Sigma$, não se sabe se a computação de M com entrada $w$ vai ou não parar.
• (B) O problema da parada é indecidível.
• (C) Não existe algoritmo que determina quando uma gramática livre de contexto arbitrária é ambígua.
• (D) Não existe autômato finito determinístico que reconheça alguma linguagem livre de contexto.
• (E) Um autômato com duas pilhas pode ser simulado por uma máquina de Turing.

Resolução

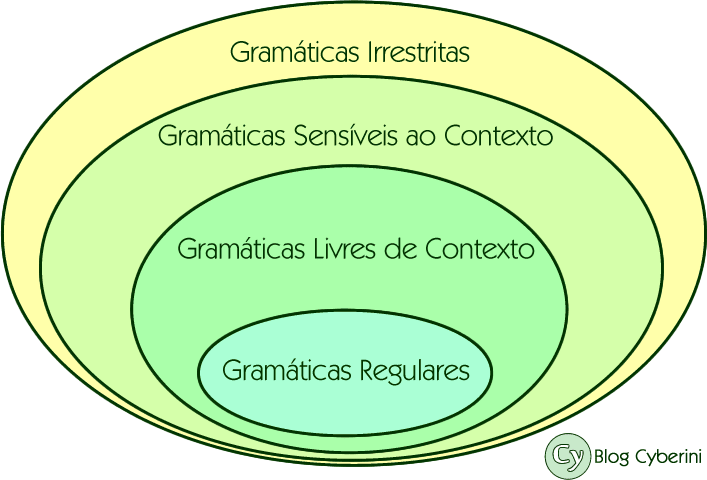
A única alternativa falsa é a D. Linguagens regulares são reconhecidas por autômatos finitos determinístico e, pela hierarquia de Chomsky, toda linguagem regular também é livre de contexto.

Hierarquia de Chomsky (Clique aqui para ampliar)

POSCOMP 2007

A questão a seguir é do ano 2007.

Questão 26

Seja a linguagem formal $L = \{a^nb^{2n}c,n\geq 0\}$. Analise as seguintes assertivas.

• I. $L$ é uma linguagem livre de contexto.
• II. A gramática $G=\left(\{S,X\},\{a,b,c\},\{S\rightarrow Xc, X\rightarrow aXbb|\epsilon\},S\right)$ gera a linguagem $L$.
• III. $L$ não pode ser reconhecida por um autômato com pilha.

A análise permite concluir que estão CORRETAS

• (A) apenas as assertivas I e II.
• (B) apenas as assertivas I e III.
• (C) apenas as assertivas II e III.
• (D) todas as assertivas.
• (E) nenhuma das assertivas.

Resolução

As afirmativas I e II estão corretas. A gramática G é livre de contexto e produz corretamente a linguagem L.

A produção $X\rightarrow aXbb|\epsilon$ produz $a^nb^{2n}$, isto é, para cada a à esquerda, teremos dois b's à direita. Essa "simetria" não pode ser expressa por uma gramática regular.

Uma vez que a gramática G é livre de contexto, então a linguagem L, produzida por G, é livre de contexto.

A afirmativa III está incorreta, pois como a linguagem L é livre de contexto, então ela é reconhecida por um autômato com pilha.

Portanto, a alternativa correta é a A.

POSCOMP 2008

As questões a seguir são do POSCOMP 2008.

Questão 30

Analise as seguintes afirmativas.

• I. Todo autômato finito não-determinístico pode ser simulado por um autômato finito determinístico.
• II. Todo autômato finito determinístico pode ser simulado por um autômato finito não-determinístico.
• III. Todo autômato finito não-determinístico pode ser simulado por um autômato de pilha determinístico.
• IV. Todo autômato de pilha determinístico pode ser simulado por um autômato finito não-determinístico.
• V. Todo autômato finito não-determinístico pode ser simulado por uma máquina de Turing determinística.

A análise permite concluir que estão CORRETAS

• (A) apenas as afirmativas I, II, III e IV.
• (B) apenas as afirmativas II, III e V.
• (C) apenas as afirmativas I, II, III e V.
• (D) apenas as afirmativas II e IV.
• (E) apenas as afirmativas I, II e IV.

Resolução

A única afirmativa falsa é a IV. Autômatos de pilha reconhecem linguagens livres de contexto, enquanto que autômatos finitos reconhecem linguagens regulares.

Portanto, é impossível simular um autômato de pilha utilizando um autômato finito, pois a classe de linguagens que esse último reconhece é hierarquicamente inferior.

Além disso, autômatos finitos não possuem memória auxiliar para simular a pilha.

Logo, a alternativa correta é a C.

Questão 42

Analise as seguintes igualdades de expressões regulares:

• I. $a^{*} = (a^{*})^{*}$
• II. $(a+b)^{*} = (b+a)^{*}$
• III. $a^{*}+b^{*} = (a+b)^{*}$

A análise permite concluir que

• (A) somente as igualdades I e II são verdadeiras.
• (B) somente a igualdade I é verdadeira.
• (C) somente as igualdades II e III são verdadeiras.
• (D) todas as igualdades são verdadeiras.
• (E) nenhuma das igualdades é verdadeira.

Resolução

Nas afirmativas II e III o operador "+" não é o fecho positivo e sim o operador de união. Podemos reescrever as afirmativas da seguinte forma:

• II. $(a|b)^{*}=(b|a)^{*}$
• III. $a^{*}|b^{*}=(a|b)^{*}$

A afirmativa I está correta (é trivial).

A afirmativa II também está correta (também é trivial, pois o operador de união "|" é comutativo).

A afirmativa III está errada. Enquanto a expressão regular à esquerda reconhece cadeias contendo apenas a's ou cadeias contendo apenas b's, a expressão regular à direita reconhece qualquer cadeia de a's e b's. Por exemplo, a cadeia aab é reconhecida por $(a|b)^{*}$, mas não é reconhecida por $a^{*}|b^{*}.$

Portanto, a alternativa correta é a A.