Questões do POSCOMP sobre Linguagens Formais e Autômatos #01

As questões desta postagem são das provas do POSCOMP dos anos 2002, 2003 e 2004 sobre Linguagens Formais e Autômatos.

Para mais questões resolvidas, acesse a página POSCOMP.

POSCOMP 2002

As questões a seguir são da prova do ano 2002.

Questão 25

Assinale quantas sequências de caracteres a seguir são reconhecidas pelo autômato finito abaixo. As quatro sequências de caracteres (separadas por vírgulas) são: 0, +567, -89.5, -3e3.

Clique aqui para ampliar

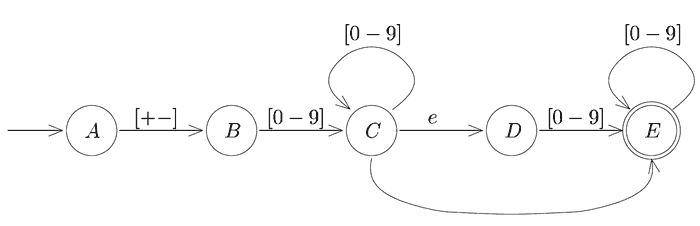
• (A) 0
• (B) 1
• (C) 2
• (D) 3
• (E) 4

Resolução

Primeiramente, observe que toda cadeia reconhecida pelo autômato deve iniciar com o sinal "+" ou com o sinal "-". Portanto, o autômato não reconhece 0 (zero).

Observe também que não é possível gerar ponto (.). Logo, a cadeia -89.5 não é reconhecida.

As demais cadeias (+567 e -3e3) são reconhecidas.

Portanto, a alternativa correta é a C.

Questão 26

Sobre a hierarquia de Chomsky podemos afirmar que:

• (A) Uma linguagem que é recursivamente enumerável não pode ser uma linguagem regular
• (B) As linguagens livres de contexto e as linguagens sensíveis ao contexto se excluem
• (C) Uma linguagem que não é regular é livre de contexto
• (D) As linguagens reconhecidas por autômatos a pilha são as linguagens regulares
• (E) Há linguagens que não são nem livres de contexto nem sensíveis ao contexto

Resolução

A alternativa A é falsa. Segue o teorema das linguagens recursivamente enumeráveis:

Teorema: Qualquer linguagem gerada por uma gramática irrestrita é recursivamente enumerável [1].

Uma das consequências desse teorema é que todas as linguagens regulares são recursivamente enumeráveis, uma vez que toda gramática regular também é irrestrita.

Hierarquia de Chomsky (Clique aqui para ampliar)

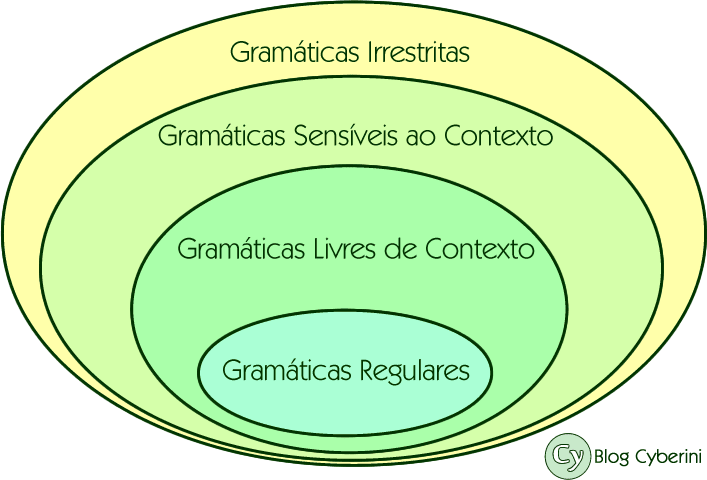
Toda linguagem livre de contexto também é sensível ao contexto, portanto a alternativa B é falsa.

A alternativa C está errada porque quando uma linguagem não é regular, ela também pode ser sensível ao contexto ou irrestrita.

A alternativa D está errada. As linguagens reconhecidas por autômatos a pilha são linguagens livres de contexto. Apesar das linguagens regulares também serem livres de contexto e, portanto, também serem reconhecidas por um autômato a pilha, a afirmação exclui as linguagens que são puramente livres de contexto.

A alternativa E está correta. Tais linguagens são irrestritas (ou estruturadas em frase).

POSCOMP 2003

As questões a seguir são da prova do ano 2003.

Questão 27

Uma gramática G é definida por

$$G=\left(\{x,y,z\},\{S,W,X,Y,Z\},P,S\right)$$

na qual os membros de P são

$$\begin{align*}&S\rightarrow WZ\\&W\rightarrow X\,|\,Y\\&X\rightarrow x\,|\,xX\\&Y\rightarrow y\,|\,yY\\&Z\rightarrow z\,|\,zZ\end{align*}$$

Qual das expressões regulares abaixo corresponde a esta gramática?

• (A) $(xx^{*}\,|\, yy^{*})zz^{*}$
• (B) $xx^{*}\,|\,yy^{*}\,|\,zz^{*}$
• (C) $xx^{*}(yy^{*}\,|\,zz^{*})$
• (D) $(xx\,|\,yy)^{*}zz^{*}$
• (E) $xx^{*}yy^{*}zz^{*}$

Resolução

Os símbolos não terminais $X$, $Y$ e $Z$ produzem, respectivamente, $xx^{*}$, $yy^{*}$ e $zz^{*}$. Além disso, podemos eliminar $W$ substituindo-o na primeira produção:

$$\begin{align*}S&\rightarrow (X\,|\,Y)Z\\X&\rightarrow xx^{*}\\Y&\rightarrow yy^{*}\\Z&\rightarrow zz^{*}\end{align*}$$

Substituindo $X$, $Y$ e $Z$ na primeira produção, obtemos

$$S\rightarrow\left(xx^{*}\,|\,yy^{*}\right)zz^{*}$$

Portanto, a alternativa correta é a A.

Questão 46

Considere as seguintes afirmações sobre autômatos finitos e expressões regulares:

I A classe de linguagens aceita por um Autômato Finito Determinístico (AFD) não é a mesma que um Autômato Finito Não Determinístico (AFND).

II Para algumas expressões regulares não é possível construir um AFD.

III A expressão regular $(b+ba)+$ aceita os "strings" de b's e a's começando com b e não tendo dois a's consecutivos.

Selecione a afirmativa correta:

• (A) As afirmativas I e II são verdadeiras
• (B) As afirmativas I e III são falsas
• (C) Apenas a afirmativa III é verdadeira
• (D) As afirmativas II e III são falsas
• (E) As afirmativas I e III são verdadeiras

Resolução

A primeira afirmação é falsa porque AFDs e AFNDs reconhecem a mesma classe de linguagens (linguagens regulares). Além disso, essas duas classes de autômatos são equivalentes.

A afirmativa II também é falsa. Toda expressão regular representa uma linguagem regular que, consequentemente, é reconhecida por um AFD. Logo, é sempre possível construir um AFD para uma expressão regular.

A afirmativa III está correta. O único problema é a notação utilizada na expressão regular, que causa confusão. A ER pode ser escrita da seguinte forma: $(b\,|\,ba)^{+}$. Observe que toda cadeia reconhecida pela ER inicia com b e que não é possível ter dois a's consecutivos.

Portanto, a alternativa correta é a C.

POSCOMP 2004

A questão a seguir é do ano 2004.

Questão 21

Seja $\Sigma=\{a,b\}$. Uma expressão regular denotando a linguagem L = {$w\in\Sigma^{*}$ tal que toda ocorrência de "a" em $w$ é imediatamente seguida de "b"} é:

• (A) $(a^{*}b)^{*}$
• (B) $(b+ab)^{*}$
• (C) $a^{*}b$
• (D) $b+(ab)^{*}$
• (E) $(ab)^{*}$

Resolução

As alternativas A e C estão incorretas, pois as expressões regulares reconhecem, por exemplo, a cadeia aab, que não faz parte da linguagem do enunciado.

A alternativa E também está errada. O problema é que ela não reconhece todas as cadeias da linguagem do enunciado. Por exemplo, a cadeia bab faz parte de L, mas não é reconhecida pela ER.

A alternativa D está errada. Entretanto, a ER dessa alternativa é confusa, pois não temos como saber se o operador "+" é o fecho positivo ou o operador de união, que é normalmente representado por "|". Felizmente, em ambos os casos a alternativa estaria errada.

Portanto, a única alternativa correta é a B.

Referências

[1] ROSA, J. L. C. (2010). SCC-205 - Capítulo 4 Linguagens Recursivamente Enumeráveis e Máquinas de Turing. ICMC/USP - São Carlos. Disponível em: <http://wiki.icmc.usp.br/images/a/a3/SCC205Cap4.pdf>. Acesso em 17 de novembro de 2017.