Introdução
Para quem não conhece, o Teorema de Laplace tem como finalidade o cálculo de determinantes de matrizes de qualquer ordem.
Em geral, no ensino médio, aprendemos a calcular determinantes de matrizes de ordem dois e de ordem três (Regra de Sarrus) e alguns artifícios para cálculos de determinantes, como redução de ordem da matriz se a mesma obedece a certas condições (Regra de Chió, por exemplo).

Entretanto, de forma geral, para matrizes de ordem quatro ou superior temos que usar o Teorema de Laplace para calcular o determinante. Abaixo, segue um exemplo de determinante resolvido utilizando o teorema.
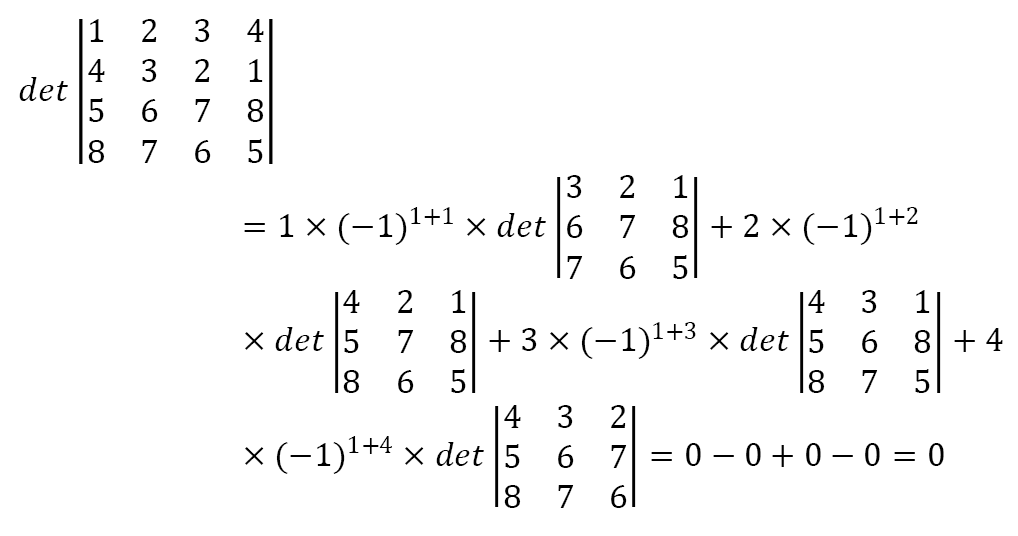
Não irei dar detalhes do teorema porque não é o objetivo da postagem.
Caso tenha interesse em aprender o teorema, recomendo o seguinte artigo do site "Brasil Escola" feito por Gabriel Alessandro de Oliveira da "Equipe Brasil Escola" (acesso em 18/11/2013): http://www.brasilescola.com/matematica/teorema-laplace.htm.
Índice
Algoritmo do Teorema de Laplace
O algoritmo a seguir escolhe sempre a primeira linha no cálculo do determinante. É recomendado conhecer previamente o Teorema de Laplace antes de analisar o algoritmo.
Utilizei recursividade. É importante salientar que o Teorema de Laplace não é um método eficiente para calcular determinantes. Na prática, sua complexidade no tempo é de O(n!), que é pior que a complexidade exponencial.
Além disso, ele tem um custo grande de memória também, pois a cada chamada recursiva ele aloca memória para as matrizes que serão utilizadas no cálculo dos cofatores. Em síntese, não utilize este algoritmo em situações práticas. Ele é útil para fins didáticos ou para calcular determinantes de matrizes pequenas.
Se você precisar de um método mais eficiente, você pode utilizar a decomposição LU (ou LUP) combinada com o Teorema de Binet. Esse é o método mais eficiente que eu conheço (pelo menos até a escrita deste texto).
/** * * @author Henrique Felipe */ public class TeoremaDeLaplace { public static double laplace(double[][] matriz) { //parte-se do pressuposto que a matriz seja válida double determinante = 0;//valor do determinante que vai ser retornado if (matriz.length == 1) { //calcula o determinante de matriz de ordem um determinante = matriz[0][0]; } else if (matriz.length == 2) { //calcula o determinante de matriz de ordem dois determinante = matriz[0][0] * matriz[1][1] - matriz[0][1] * matriz[1][0]; } else if (matriz.length == 3) { //calcula o determinante de matriz de ordem três usando regra de Sarrus determinante = matriz[0][0] * matriz[1][1] * matriz[2][2] + matriz[0][1] * matriz[1][2] * matriz[2][0] + matriz[0][2] * matriz[1][0] * matriz[2][1] - matriz[0][2] * matriz[1][1] * matriz[2][0] - matriz[0][0] * matriz[1][2] * matriz[2][1] - matriz[0][1] * matriz[1][0] * matriz[2][2]; } else { /* Os termos elemento-pivô, pivô, linha-pivô são usados para fazer * referência a linha/coluna (nesse caso, linha 0) que foi usada * de base para o cálculo do determinante e também para se referir aos * elementos da linha/coluna em questão * * O termo matriz principalé usado para fazer referência a matriz que * vamos calcular o determinante * * O termo matriz auxilixar é usado para fazer referência as matrizes * de ordem reduzida que surgem, em consequência do teorema, para calcular * o determinante da matriz principal */ /* * Essa matriz auxiliar foi criada porque, para calcular o determinante * de uma matriz de ordem 'n', precisaremos calcular 'n' determinantes * de matrizes de ordem n-1. * Ou seja, essa matriz auxiliar será, a cada ciclo, uma dessas matrizes * de ordem n-1 * * Serão 'n' ciclos. A cada ciclo, preencheremos essa matriz auxiliar * com os valores da matriz principal, exceto os elementos que pertencem à * mesma linha ou à mesma coluna. * * Para fazer o preenchimento da matriz auxiliar precisaremos percorrer * a matriz principal, ou seja, teremos um ciclo duplo. Nesse ciclo iremos * ignorar todos os elementos que pertencem a mesma linha ou coluna do * elemento-pivô correpondente. Como a matriz auxiliar é de ordem reduzida * usaremos duas novas variáveis 'i_aux' e 'j_aux' que representarão, * respectivamente, o índice da linha e o índice da coluna da matriz auxiliar */ double[][] aux; int i_aux, j_aux, linha, coluna, i; //esse loop irá fazer uma varredura coluna-coluna na primeira linha da matriz //isso, porque escolhemos a primeira linha como pivô fixo for (i = 0; i < matriz.length; i++) { /* * Verifica se o elemento-pivô é diferente de zero para poder fazer * todo o calculo. * Caso o elemento seja zero, não há necessidade de fazer o cálculo * afinal todo o produto irá zerar. Também não precisaremos fazer a soma * parcial de zero, já que zero somado não influencia no resultado */ if (matriz[0][i] != 0) { aux = new double[matriz.length - 1][matriz.length - 1]; i_aux = 0; j_aux = 0; /*começa da linha 1, porque a linha zero é o pivo escolhido saiba que, mesmo usando como índices iniciais o valor zero, o teorema funciona perfeitamente */ for (linha = 1; linha < matriz.length; linha++) { for (coluna = 0; coluna < matriz.length; coluna++) { /* * pelo teorema de Laplace, não podemos usar elementos * da mesma linha ou coluna do pivo escolhido * Lembre-se que para cada elemento pivo, iremos ignorar * uma coluna diferente. Sabemos qual é essa coluna graças ao * ciclo mais externo, com índice i * É por isso tudo que temos esse 'if' */ if (coluna != i) { aux[i_aux][j_aux] = matriz[linha][coluna]; j_aux++; } } /* * Após percorrer uma linha inteira da matriz principal, * faz incremento de 'i_aux' para poder ir para preencher a * próxima linha. * * Zera 'j_aux' para poder começar a percorrer os elementos * da linha seguinte * * Lembre-se não podemos usar os índices da matriz principal * porque a ordem dela é superior a ordem da matriz auxiliar */ i_aux++; j_aux = 0; } /* * Calcula a parcela do pivô correspondente e soma ao valor que * será retornado. * Observe que, o método 'laplace' é chamado (recursividade) para * calcular o determinante da matriz auxiliar de ordem n-1. Isso vai * ocorrer até chegar na ordem 3, que é um caso básico, onde será usada a Regra de Sarrus, * ocorrerá o desempilhamento e, finalmente, teremos nosso * determinante * * 'matriz[0][i]' é o elemento-pivô da nossa linha-pivô zero * * 'Math.pow(-1, i)' faz parte do teorema, "se a soma do índice da linha * com o índice da coluna for par, mantemos o sinal, senão trocamos o sinal". */ determinante += Math.pow(-1, i) * matriz[0][i] * laplace(aux); } } } return determinante; } }
Observe que este algoritmo recursivo considera três casos básicos:
- quando a matriz é de ordem um (o determinante é o único elemento que a matriz possui);
- quando a matriz é de ordem dois;
- quando a matriz é de ordem três (regra de Sarrus).
Nos três casos o custo computacional é constante.
Observe também a linha do cálculo do sinal do cofator:
Math.pow(-1, i)*matriz[0][i]*laplace(aux).
Essa linha foi modificada pois o algoritmo sempre escolhe a primeira linha, cujo índice é zero (i + 0 = i).
O fato do primeiro índice das matrizes em Java ser zero é irrelevante. O sinal do cofator é dado por (-1)i+j. Se somarmos 1 (um) em cada índice para que o índice inicial seja 1 (um), então temos:
(-1)(i+1)+(j+1).
Desenvolvendo a expressão temos:
(-1)i+1+j+1
(-1)i+j+2
(-1)i+j(-1)2
(-1)i+j.
Ou seja, o deslocamento dos índices não faz diferença.
Download do Código
Clique no link a seguir para realizar o download do código fonte: Teorema de Laplace (Projeto NetBeans 8).
Decomposição LU e Teorema de Binet
Conforme mencionei antes, o Teorema de Laplace não é um método eficiente para calcular determinantes, pois a sua complexidade é de O(n!). Entretanto, é possível calcular determinantes de forma eficiente utilizando a decomposição LU e o Teorema de Binet.
A decomposição LU consiste em fatorar uma matriz quadrada A como o produto de uma matriz triangular inferior (L) e uma matriz triangular superior (U). Para isso, a matriz A não pode ser singular (se for singular, a fatoração não é única). Isto é,
A = LU.
Por outro lado, o Teorema de Binet nos diz que o determinante do produto de matrizes quadradas é igual ao produto de seus determinantes. Ou seja,
det(AB) = det(A)det(B).
Isto é, se combinarmos a decomposição LU e o Teorema de Binet, temos
det(A) = det(L)det(U).
Como L e U são matrizes triangulares, então os seus respectivos determinantes podem ser calculados em tempo O(n). Isso ocorre porque, para calcular o determinante de uma matriz triangular, basta multiplicar os elementos da diagonal principal.
Por outro lado, a decomposição LU tem complexidade igual a O(n³).
Portanto, teríamos um algoritmo com complexidade O(n³) para calcular determinantes (não precisamos considerar a complexidade O(n) do cálculo de determinantes, pois O(n³) é maior). Obviamente, um algoritmo com complexidade O(n³) é bem melhor do que um algoritmo com complexidade O(n!).
Referências
- [1] DANTE, L. R. Matemática, Volume único. 1ª edição. São Paulo: Ática, 2005.
- [2] MELO, J. P. B. C.; FILHO, V. S. Álgebra Linear. Universidade Cruzeiro do Sul - LFTC
- [3] Laplace expansion (Wikipedia). Disponível em: <https://en.wikipedia.org/wiki/Laplace_expansion>. Acesso em 20/07/2017.

Que obra prima esse artigo. Sapoha de Laplace é muito difícil de entender mas olhando via código java você já começa a ter uma clareza na mente.
ResponderExcluirObrigado por compartilhar. Apenas um comentário: creio que a linha 42 deva ser:
ResponderExcluirdeterminante += Math.pow(-1, i+1)*matriz[0][i]*laplace(aux);
a fim de adequar o sinal do cofator.
Boa noite, Pedro. Obrigado pela leitura!
ExcluirEu fiz uma atualização nesta postagem e respondi sua dúvida no meio do texto:
"O fato do primeiro índice das matrizes em Java ser zero é irrelevante. O sinal do cofator é dado por (-1)^(i+j). Se somarmos 1 (um) em cada índice para que o índice inicial seja 1 (um), então temos:
(-1)^((i+1)+(j+1)).
Desenvolvendo a expressão temos:
(-1)^(i+1+j+1)
(-1)^(i+j+2)
(-1)^(i+j)(-1)^2
(-1)^(i+j).
Ou seja, o deslocamento dos índices não faz diferença."