O produto de Kronecker é um tipo especial de produto de matrizes (produto tensorial).
Esse produto é aplicado, por exemplo, no cálculo do laplaciano discreto, que, por sua vez, é utilizado na resolução numérica de algumas equações diferenciais parciais, como a equação de Laplace.
O objetivo desta postagem é apresentar um algoritmo que permite calcular o produto de Kronecker entre duas matrizes.
Além do pseudocódigo, disponibilizarei o algoritmo codificado em Java e em C.
Também mostrarei como calcular o produto de Kronecker no MATLAB e no Octave e um exemplo de equação resolvida numericamente com o auxílio desse produto.
Produto de Kronecker
Se $A_{p\times q}$ é uma matriz com $p$ linhas e $q$ colunas e $B_{r\times s}$ é uma matriz com $r$ linhas e $s$ colunas, então o produto de Kronecker de $A$ e $B$ (denotado por $A\otimes B$) é uma matriz $C_{pr\times qs}$ com $pr$ linhas e $qs$ colunas dividida em $p\times q$ blocos. Cada bloco $(i, j)$ é uma matriz da forma $a_{ij} B$, onde $a_{ij}$ é o elemento da matriz $A$ que ocupa a linha $i$ e coluna $j$ (TREFETHEN, 2000).
Não entendeu nada? Um exemplo deixará mais claro:
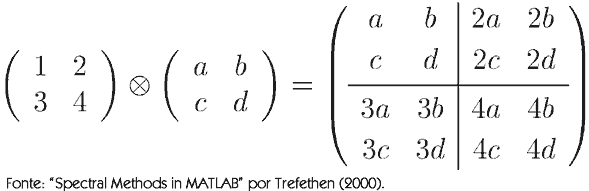
Em geral, o produto de Kronecker não é comutativo
$$A\otimes B\neq B\otimes A$$
Além disso, não há restrições em relação às dimensões de A e de B.
$$\begin{bmatrix}2\\4\end{bmatrix}\otimes\begin{bmatrix}2 & 1\\3 & 1\end{bmatrix}=\begin{bmatrix}4 & 2\\6 & 2\\\hline8 & 4\\12 & 4\end{bmatrix}$$
A maneira como os blocos são distribuídos depende da matriz A. Nesse último exemplo, a matriz A tem tamanho 2×1. Portanto, o produto conterá 2×1 blocos. O primeiro bloco (1, 1) é igual ao elemento 2 multiplicado pela matriz B. O segundo bloco (2, 1) é igual ao produto do elemento 4 por B.
Na prática, o produto de Kronecker é mais fácil do que o produto usual de matrizes. Por outro lado, seu algoritmo é um pouco mais complexo.
Os blocos mencionados ao longo do texto são apenas uma maneira de facilitar a compreensão, pois o resultado do produto $A\otimes B$ é uma matriz como qualquer outra.
Algoritmo
O algoritmo do produto de Kronecker é apresentado a seguir
1. kron(Ap×q, Br×s) 2. | inicializar a matriz Cpr×qs 3. | para i ← 1 até p 4. | | para j ← 1 até q 5. | | | row ← (i - 1) * r + 1 6. | | | para k ← até r 7. | | | | col ← (j - 1) * s + 1 8. | | | | para l ← 1 até s 9. | | | | | C(row, col) ← A(i, j) * B(k, l) 10.| | | | | col ← col + 1 11.| | | | fim_para 12.| | | | row ← row + 1 13.| | | fim_para 14.| | fim_para 15.| fim_para 16.| retorne Cpr×qs 17.fim_kron
A complexidade no tempo desse algoritmo é $O(p\times r\times q\times s)$.
Códigos
Os códigos do produto de Kronecker em Java e em C são apresentados a seguir.
Código em Java
//GitHub: HenriqueIni / www.blogcyberini.com
public class ProdutoKronecker {
//Calcula o produto de Kronecker entre A e B
public static double[][] kron(double[][] A, double[][] B){
//O código não faz validações. A e B devem ser matrizes válidas
int p = A.length;
int q = A[0].length;
int r = B.length;
int s = B[0].length;
int row, col;
//Matriz resultado
double[][] C = new double[p * r][q * s];
//Laço quádruplo aninhado: percorre as matrizes A e B
for(int i = 0; i < p; i++){
for(int j = 0; j < q; j++){
row = i * r;
for(int k = 0; k < r; k++){
col = j * s;
for(int l = 0; l < s; l++){
//Preenche a matriz C
C[row][col] = A[i][j] * B[k][l];
col++;
}
row++;
}
}
}
return C;
}
// Método auxiliar para transformar matriz em String
private static String toString(double[][] matrix){
String aux = "";
for(int i = 0; i < matrix.length; i++){
aux += "[" + matrix[i][0];
for(int j = 1; j < matrix[i].length; j++){
aux += "," + matrix[i][j];
}
aux += "]";
if(i != matrix.length - 1){
aux += "\n";
}
}
return aux;
}
//Testes
public static void main(String[] args) {
//Teste 1
double[][] A = {{2,4}};
double[][] B = {{2, 1},{3, 1}};
System.out.println(toString(kron(A, B))+"\n");
//Teste 2
double[][] C = {{1,2}};
double[][] D = {{1,3}};
double[][] E = {{1},{1}};
System.out.println(toString(kron(kron(C, D), E))+"\n");
//Teste 3
double[][] F = {{2},{4}};
System.out.println(toString(kron(F, B))+"\n");
}
}
Código em C
Observe que no código em C a matriz que vai conter os resultados deve ser passada nos parâmetros. Se você for mais familiarizado com ponteiros em C (não é o meu caso), então você pode deixar esse algoritmo mais simples ainda.
//GitHub: HenriqueIni / www.blogcyberini.com
#include <stdio.h>
#include <stdlib.h>
//Calcula o produto de Kronecker entre A e B
//O resultado é armazenado em C
//Esse método pode ser simplificado com o uso de ponteiros
void kron(int p, int q, double A[p][q],
int r, int s, double B[r][s],
int pr, int qs,double C[pr][qs]){
//O código não faz validações, logo os parâmetros devem ser válidos
int i, j, k, l, col, row;
for(i = 0; i < p; i++){
for(j = 0; j < q; j++){
row = i * r;
for(k = 0; k < r; k++){
col = j * s;
for(l = 0; l < s; l++){
//Preenche a matriz C
C[row][col] = A[i][j] * B[k][l];
col++;
}
row++;
}
}
}
}
// Função auxiliar para imprimir matrizes
void printArray(int n, int m, double A[n][m]){
int i, j;
for(i = 0; i < n; i++){
printf("[%.4f", A[i][0]);
for(j = 1; j < m; j++){
printf(",%.4f", A[i][j]);
}
printf("]");
if(i != n - 1){
printf("\n");
}
}
}
// Testes
int main() {
//Teste 1
double A[1][2] = {{2,4}};
double B[2][2] = {{2, 1},{3, 1}};
double R[2][4];
kron(1, 2, A, 2, 2, B, 2, 4, R);
printArray(2, 4, R);
printf("\n\n");
//Teste 2
double F[2][1] = {{2},{4}};
double R2[4][2];
kron(2, 1, F, 2, 2, B, 4, 2, R2);
printArray(4, 2, R2);
}
MATLAB e Octave
Os softwares MATLAB e Octave já possuem uma função para calcular o produto de Kronecker.

Em ambos os programas, o produto de Kronecker entre as matrizes A e B pode ser feito utilizando o seguinte trecho de código [2][3]:
C = kron(A, B)
Laplaciano discreto
Se $D_n^2$ é uma matriz de derivação $n\times n$ de segunda ordem em uma dimensão (isto é, ela serve para calcular a derivada de segunda ordem de uma função de uma variável), então o laplaciano discreto em duas dimensões será [1]
$$L_n=I_n\otimes D_n^2 + D_n^2\otimes I_n$$
$I_n$ é a matriz identidade de ordem $n$. Em três dimensões, teríamos
$$L_n=I_n\otimes I_n\otimes D_n^2 + I_n\otimes D_n^2\otimes I_n + D_n^2\otimes I_n\otimes I_n$$
Nos dois exemplos, estou supondo que uma mesma matriz de derivação é utilizada para derivar em todas as dimensões.
Aplicação
O exemplo a seguir foi retirado do livro "Spectral Methods in MATLAB" por Trefethen (2000).
No exemplo, Trefethen resolve numericamente a equação de Poisson $\nabla^2 u = 10\operatorname{sin}(8x(y - 1))$ no retângulo $[-1,1]\times[-1,1]$, onde a função $u$ é igual a zero na fronteira.
Para resolver a equação, o laplaciano discreto é calculado utilizando o produto de Kronecker.
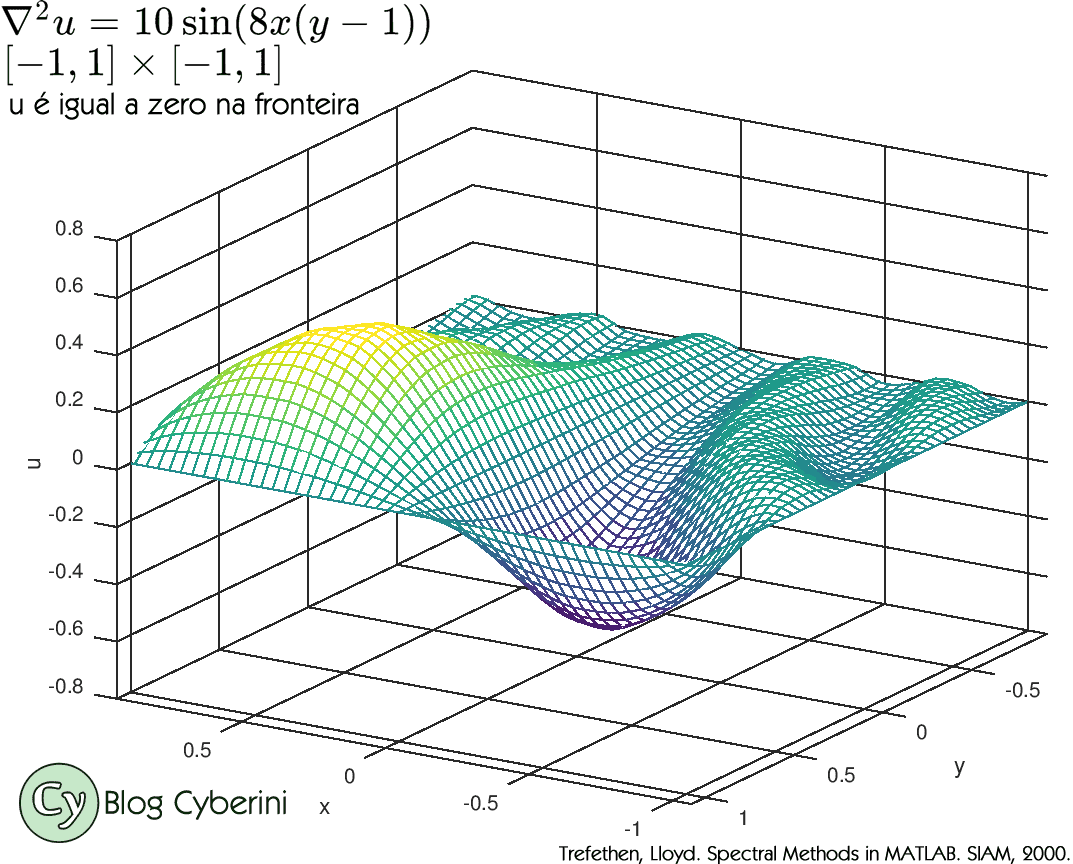
O programa utilizado nos cálculos pode ser obtido no link: Equação de Poisson (Octave). Eu fiz algumas modificações para que o programa funcionasse no Octave, uma vez que o original foi escrito para MATLAB.
Se quiser uma visão mais ampla desse gráfico, assista ao vídeo: gráfico da solução da equação (YouTube).
Leia também
Referências
- [1] Trefethen, Lloyd. Spectral Methods in MATLAB. SIAM, 2000.
- [2] Octave DOCS: 18.4 Functions of a Matrix. Acesso em 16 de abril de 2018.
- [3] MathWorks: kron. Acesso em 16 de abril de 2018.

Nenhum comentário:
Postar um comentário