Questões do POSCOMP sobre Complexidade de Algoritmos #02

Esta postagem é a continuação da postagem Questões do POSCOMP sobre Complexidade de Algoritmos #01, onde apresento a solução de algumas questões do POSCOMP sobre Complexidade de Algoritmos.

Para mais questões sobre o exame acesse a página POSCOMP.

POSCOMP 2006

Questão 25

Dada uma lista linear de $n+1$ elementos ordenados e alocados sequencialmente, qual é o número médio (número esperado) de elementos que devem ser movidos para que se faça uma inserção na lista, considerando-se igualmente prováveis as $n+1$ posições de inserção?

• (A) $n/2$
• (B) $(n+2)/2$
• (C) $(n-1)/2$
• (D) $n(n+3+2/n)/2$
• (E) $(n+1)/2$

Resolução

Como todas as posições de inserção são igualmente prováveis, então a probabilidade de uma posição ser a posição de inserção é igual a $1/(n+1)$.

Suponhamos que o deslocamento seja para a direita. Então, para inserir um elemento na primeira posição, teríamos $n + 1$ deslocamentos. Se a inserção fosse na segunda posição, então seriam n deslocamentos. Seguindo essa lógica, o valor esperado será

$$E=\frac{1}{n+1}\sum_{i=1}^{n+1}(n+2-i)$$

$$E=\frac{1}{n+1}\left[(n+2)(n+1)-\frac{(n+1)(n+2)}{2}\right]$$

$$E=n+2-\frac{(n+2)}{2} = \frac{n+2}{2}$$

Se optássemos pelo deslocamento à esquerda, então a fórmula seria

$$E=\frac{1}{n+1}\sum_{i=1}^{n+1}i$$

$$E=\frac{1}{n+1}\frac{(n+1)(n+2)}{2}=\frac{n+2}{2}$$

Ou seja, o mesmo resultado. Portanto, a alternativa correta é a B.

Questão 29

Considere a função Pot que calcula $x^n$, para $x$ real e $n$ inteiro:

Seja $T(n)$ o tempo de execução da função Pot para as entradas $x$ e $n$. A ordem de $T(n)$ é.

• (A) $T(n) = O(1)$
• (B) $T(n) = O(\log n)$
• (C) $T(n) = O(n)$
• (D) $T(n) = O(n\log n)$
• (E) $T(n) = O(n^2)$

Resolução

Primeiramente, observe que o custo por chamada recursiva é constante: não há laços de repetição e a chamada de outras funções tem custo constante (sqr(x) = x2).

Em segundo lugar, a cada chamada recursiva, o expoente $n$ é reduzido pela metade (ou aproximadamente pela metade, se $n$ for ímpar).

Portanto, a equação de recorrência do algoritmo é

$T(n) = T(n/2) + c$ (c é uma constante).

Na prática, é a mesma equação de recorrência da pesquisa binária. Portanto, $T(n) = O(\log n)$. Esse resultado pode ser obtido via teorema mestre:

$$\log_2 1 = 0$$

$$f(n) = c = \Theta(n^0) = \Theta(1)$$

$$T(n) = \Theta(n^0 \log n) = \Theta(\log n) \Rightarrow T(n) = O(\log n)$$

Portanto, a alternativa correta é a B.

Questão 31

Quais algoritmos de ordenação têm complexidade $O(n \log n)$ para o melhor caso, onde n é o número de elementos a ordenar.

• (A) Insertion Sort e Quicksort
• (B) Quicksort e Heapsort
• (C) Bubble Sort e Insertion Sort
• (D) Heapsort e Insertion Sort
• (E) Quicksort e Bubble Sort

Resolução

Listando o melhor caso de cada algoritmo, temos:

1. Insertion Sort: $O(n)$
2. Quicksort: $O(n \log n)$
3. Bubble Sort: $O(n)$
4. Heapsort: $O(n \log n)$

Portanto, apenas o Quicksort e o Heapsort têm complexidade $O(n \log n)$ no melhor caso. Logo, a alternativa correta é a B.

POSCOMP 2007

Questão 31

Considere o problema do caixeiro viajante, definido como se segue.

Sejam $S$ um conjunto de $n ≥ 0$ cidades, e $d_{ij} > 0$ a distância entre as cidades $i$ e $j$, $i,j \in S$, $i \neq j$. Define-se um percurso fechado como sendo um percurso que parte de uma cidade $i\in S$, passa exatamente uma vez por cada cidade de $S\backslash\{i\}$, e retorna à cidade de origem. A distância de um percurso fechado é definida como sendo a soma das distâncias entre cidades consecutivas no percurso. Deseja-se encontrar um percurso fechado de distância mínima. Suponha um algoritmo guloso que, partindo da cidade 1, move-se para a cidade mais próxima ainda não visitada e que repita esse processo até passar por todas as cidades, retornando à cidade 1.

Considere as seguintes afirmativas.

• I. Todo percurso fechado obtido com esse algoritmo tem distância mínima.
• II. O problema do caixeiro viajante pode ser resolvido com um algoritmo de complexidade linear no número de cidades.
• III. Dado que todo percurso fechado corresponde a uma permutação das cidades, existe um algoritmo de complexidade exponencial no número de cidades para o problema do caixeiro viajante.

Em relação a essas afirmativas, pode-se afirmar que

• (A) I é falsa e III é correta.
• (B) I, II e III são corretas.
• (C) apenas I e II são corretas.
• (D) apenas I e III são falsas.
• (E) I, II e III são falsas.

Resolução

Vamos analisar cada afirmativa:

(I) É falsa, pois nem sempre é possível obter um percurso de distância mínima com o algoritmo proposto no enunciado. Para exemplificar, vamos considerar o grafo a seguir:

Aplicando o algoritmo do enunciado no vértice 1, obtemos o seguinte percurso (desculpe-me pelo abuso de notação):

1 → 2 → 3 → 4 → 1

E a distância total é igual a 25. Obviamente, esse percurso não tem distância mínima.

(II) É falsa. Não existe algoritmo com complexidade linear capaz de resolver o problema do caixeiro viajante.

(III) É verdadeira. O algoritmo teria que verificar a distância de cada percurso possível para determinar aquele que possui distância mínima. Checar todas as combinações possíveis requer tempo exponencial.

Portanto, a alternativa correta é a A.

Questão 32

Observe as funções representadas no gráfico abaixo.

Gráfico da questão 32 do POSCOMP 2007

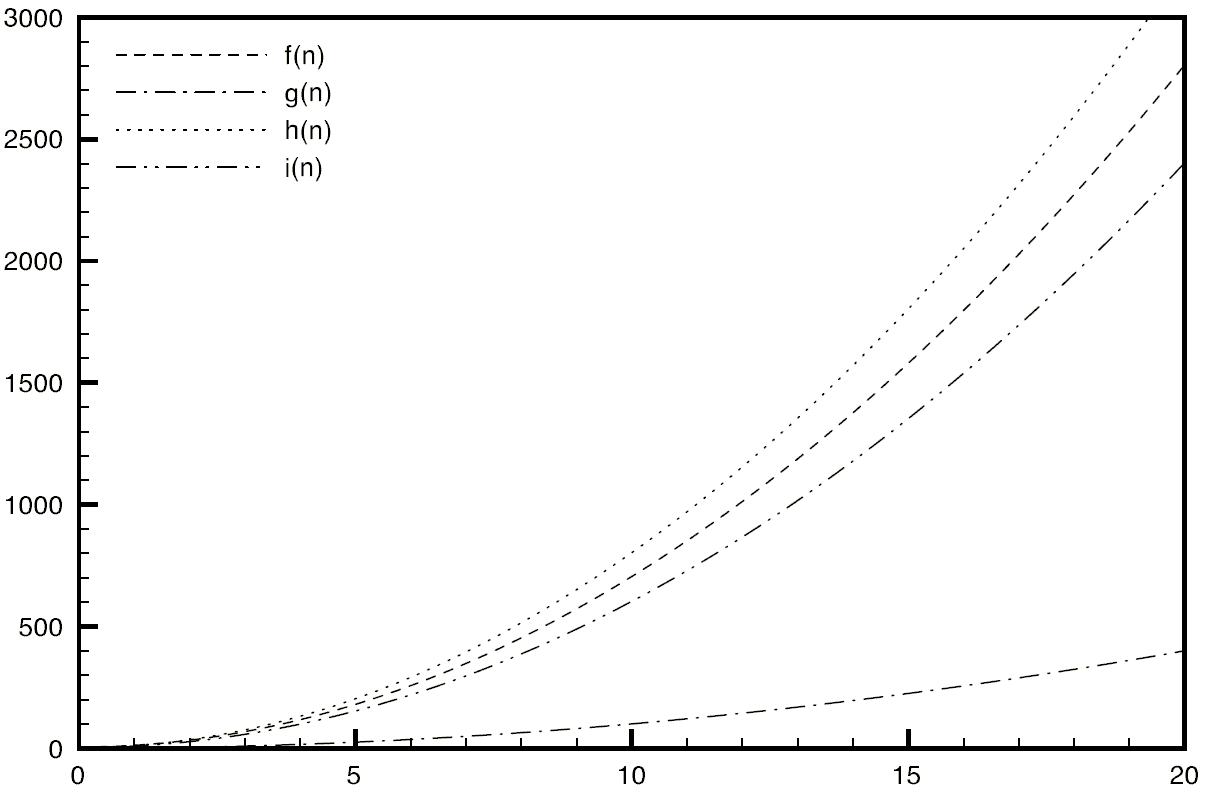
Assinale a afirmativa FALSA sobre o crescimento assintótico dessas funções.

• (A) $f(n)=O(h(n))$ e $i(n)=\Omega (g(n))$.
• (B) $f(n)=\Theta(h(n))$ e $i(n)=\Omega (h(n))$.
• (C) $g(n)=O(i(n))$ e $h(n) = \Omega(g(n))$.
• (D) $g(n)=O(i(n))$, $i(n)=O(f(n))$ e, portanto, $g(n)=O(f(n))$.
• (E) $h(n)=\Omega (i(n))$, logo, $i(n)=O(h(n))$.

Resolução

A questão em si é fácil, o único problema dela é que requer que você tenha decorado aprendido as notações assintóticas.

Irei apenas analisar a alternativa (b), que é a correta, explicando porque a afirmação é falsa.

Quando afirmamos que $f(n) = \Theta(h(n))$, significa que $f(n) = O(h(n))$ e $f(n) = \Omega (h(n))$. Analisando apenas o gráfico, vemos que, de fato, $f(n) = O(h(n))$, porém não podemos afirmar que $f(n) = \Omega (h(n))$. Além disso, observe que $i(n)\neq \Omega(h(n))$, pois $i(n)\leq h(n)$. Portanto, a alternativa correta é a B.